R语言多元线性回归

简单看一下作业的介绍：

案例 1. 多重线性回归
活动类型: 团体
交割日期：2021年12月12 日西班牙时间截止时间 23:59
最大长度： 20 张幻灯片（每个团队成员至少一张）
目标：开发一个多元线性回归模型，该模型将小组选择的数据库中的三个变量（一个因变量和两个自变量）联系起来。最少 20 次观察。我建议您留下两个观察结果来进行预测。使用 R。
结构和内容：
简介：数据库的目标和简要说明（来源和选择数据库的原因）
规格。所选主题的简要理论发展。变量和数学函数
基础数据处理（即，它将允许回答：是否存在非典型数据？是否存在缺失数据？变量之间是否存在关系？是否需要消除任何变量？）以及对所提出模型的估计和估计参数的解释
模型的验证或确认
预测
脚本
要开展这项活动，我建议您遵循已解决的【销售广告费用模型】的步骤。
最高评分 10 分，分配如下：
内容最高评价
介绍 1 分
规格 1 分
基本处理、估计和解释 3分
查看 2.5分
预言 1 分
脚本 1.5分

内容	最高评价
介绍	1 分
规格	1 分
基本处理、估计和解释	3分
查看	2.5分
预言	1 分
脚本	1.5分

数据来自：https://www.kaggle.com/econdata/climate-change

设置程序内的语言：

1
2
Sys.setlocale("LC_TIME", "English")
options(stringsAsFactors = FALSE)

导入所需要的包

1
2
3
library(xts)
library(ggplot2)
library(reshape2)

读取数据并进行预览和检查数据类型

1
2
3
csv_data <- read.csv("./climate_change.csv", header=TRUE, sep=",")
head(csv_data, 20)
str(csv_data)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
      Date    CO2     CH4   Temp     N2O
1  1983-05 345.96 1638.59  0.109 303.677
2  1983-06 345.52 1633.71  0.118 303.746
3  1983-07 344.15 1633.22  0.137 303.795
4  1983-08 342.25 1631.35  0.176 303.839
5  1983-09 340.17 1648.40  0.149 303.901
6  1983-10 340.30 1663.79  0.093 303.970
7  1983-11 341.53 1658.23  0.232 304.032
8  1983-12 343.07 1654.31  0.078 304.082
9  1984-01 344.05 1658.98  0.089 304.130
10 1984-02 344.77 1656.48  0.013 304.194

创建一些变量

1
2
3
4
5
Date <- csv_data$Date
Temp <- csv_data$Temp
CH4 <- csv_data$CH4
CO2 <- csv_data$CO2
N2O <- csv_data$N2O

设置日期为索引和没有日期的 datafram，并查看最大值、最小值、方差等等

1
2
3
4
5
format_date <- as.Date(paste0(as.character(csv_data[,1]), "-01"), format='%Y-%m-%d')
data <- xts(csv_data[,-1], order.by = format_date)
head(data, 10)
mdata <- data.frame(Temp, CH4, CO2, N2O)
summary(mdata)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
              CO2     CH4  Temp     N2O
1983-05-01 345.96 1638.59 0.109 303.677
1983-06-01 345.52 1633.71 0.118 303.746
1983-07-01 344.15 1633.22 0.137 303.795
1983-08-01 342.25 1631.35 0.176 303.839
1983-09-01 340.17 1648.40 0.149 303.901
1983-10-01 340.30 1663.79 0.093 303.970
1983-11-01 341.53 1658.23 0.232 304.032
1983-12-01 343.07 1654.31 0.078 304.082
1984-01-01 344.05 1658.98 0.089 304.130
1984-02-01 344.77 1656.48 0.013 304.194

1
2
3
4
5
6
7
      Temp              CH4            CO2             N2O       
 Min.   :-0.2820   Min.   :1630   Min.   :340.2   Min.   :303.7
 1st Qu.: 0.1217   1st Qu.:1722   1st Qu.:353.0   1st Qu.:308.1
 Median : 0.2480   Median :1764   Median :361.7   Median :311.5
 Mean   : 0.2568   Mean   :1750   Mean   :363.2   Mean   :312.4
 3rd Qu.: 0.4073   3rd Qu.:1787   3rd Qu.:373.5   3rd Qu.:317.0  
 Max.   : 0.7390   Max.   :1814   Max.   :388.5   Max.   :322.2

创建每个变量的时间序列，这里的 png() 和 dev.off() 用于将生成的图片保存到本地，你也可以删除它直接在 R 语言程序中预览

由于作业需要，我创建了四张图片，你也可以将四张表格放在一张图片上。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 温度时间序列
png(file = "./images/time_series_Temp.png", width = 800, height = 525, res = 100)
par(oma=c(2,2,2,2))
time_series_Temp <- xts(Temp, order.by = format_date)
    (time_series_Temp, main="Series temporales de temperatura", xlab="Date", ylab="Temp")
dev.off()

# CO2时间序列
png(file = "./images/time_series_CO2.png", width = 800, height = 525, res = 100)
par(oma=c(2,2,2,2))
time_series_CO2 <- xts(CO2, order.by = format_date)
plot(time_series_CO2, main="Series temporales de CO2", xlab="Date", ylab="CO2")
dev.off()

# CH4时间序列
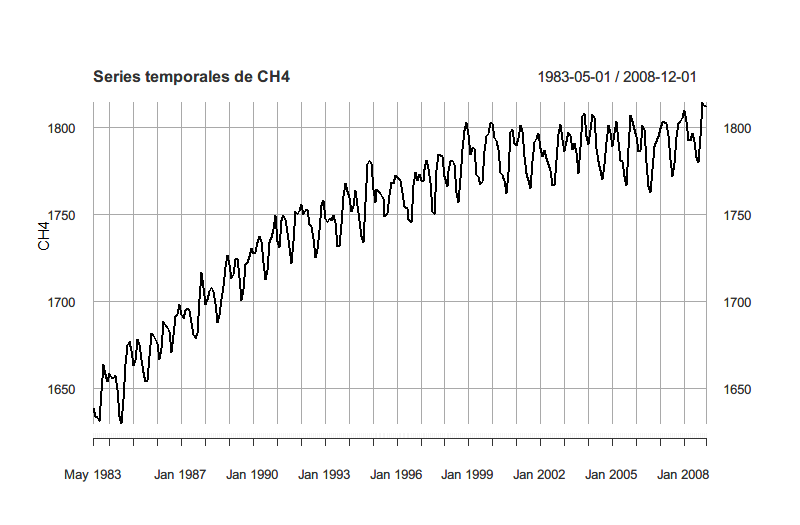
png(file = "./images/time_series_CH4.png", width = 800, height = 525, res = 100)
par(oma=c(2,2,2,2))
time_series_CH4 <- xts(CH4, order.by = format_date)
plot(time_series_CH4, main="Series temporales de CH4", xlab="Date", ylab="CH4")
dev.off()

# N2O时间序列
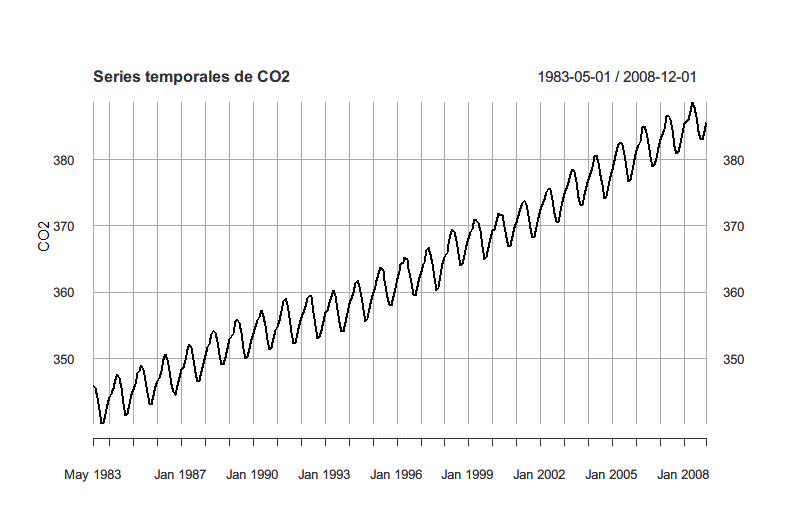
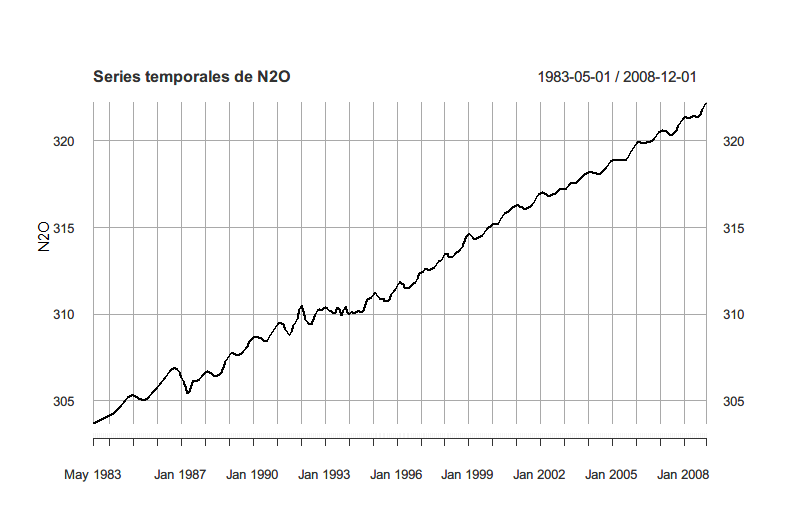
png(file = "./images/time_series_N2O.png", width = 800, height = 525, res = 100)
par(oma=c(2,2,2,2))
time_series_N2O <- xts(N2O, order.by = format_date)
plot(time_series_N2O, main="Series temporales de N2O", xlab="Date", ylab="N2O")
dev.off()

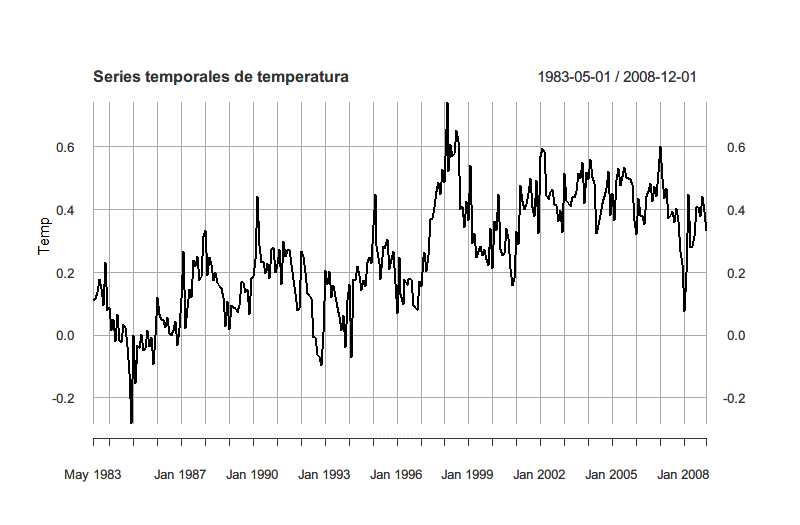
创建所有变量之间的关系图

1
2
3
4
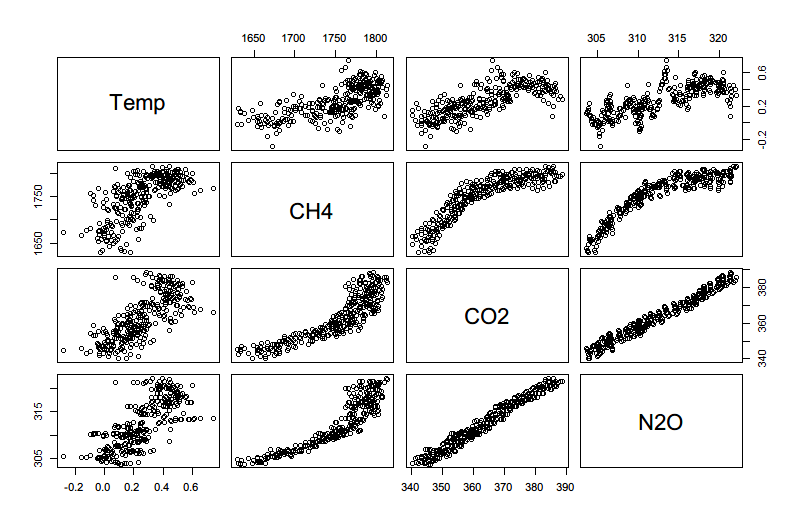
png(file = "./images/correlation_all.png", width = 800, height = 525, res = 100)
par(oma=c(2,2,2,2))
plot(mdata)
dev.off()

创建每个变量之间的散点图

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 散点图 温度-N2O
png(file = "./images/scatter_Temp_N2O.png", width = 600, height = 525, res = 100)
par(oma=c(1,1,1,1))
model_Temp_y_N2O <- lm(Temp~N2O, data=mdata)
coef <- coef(model_Temp_y_N2O)
eq = paste('y =', round(coef(model_Temp_y_N2O)[[2]], 3), 'x', '+', round(coef(model_Temp_y_N2O)[[1]], 3))
plot(N2O, Temp, xlab="N2O", ylab="Temperatura", pch=20, main="N2O y Temperatura")
abline(model_Temp_y_N2O, col="red")
mtext(eq, side = 3, line=1, adj = 0, padj = 1, col="blue")
dev.off()

# 散点图 温度-CH4
png(file = "./images/scatter_Temp_CH4.png", width = 600, height = 525, res = 100)
par(oma=c(1,1,1,1))
model_Temp_y_CH4 <- lm(Temp~CH4, data=mdata)
coef <- coef(model_Temp_y_CH4)
eq = paste('y =', round(coef(model_Temp_y_CH4)[[2]], 3), 'x', '+', round(coef(model_Temp_y_CH4)[[1]], 3))
plot(CH4, Temp, xlab="CH4", ylab="Temperatura", pch=20, main="CH4 y Temperatura")
abline(model_Temp_y_CH4, col="red")
mtext(eq, side = 3, line=1, adj = 0, padj = 1, col="blue")
dev.off()

# 散点图 温度-CO2
png(file = "./images/scatter_Temp_CO2.png", width = 600, height = 525, res = 100)
par(oma=c(1,1,1,1))
model_Temp_y_CO2 <- lm(Temp~CO2, data=mdata)
coef <- coef(model_Temp_y_CO2)
eq = paste('y =', round(coef(model_Temp_y_CO2)[[2]], 3), 'x', '+', round(coef(model_Temp_y_CO2)[[1]], 3))
plot(CO2, Temp, xlab="CO2", ylab="Temperatura", pch=20, main="CO2 y Temperatura")
abline(model_Temp_y_CO2, col="red")
mtext(eq, side = 3, line=1, adj = 0, padj = 1, col="blue")
dev.off()

创建直方图

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 因变量(温度)直方图
png(file = "./images/hist_Temp.png", width = 800, height = 525, res = 100)
par(oma=c(2,2,2,2))
hist(Temp, breaks=100, col="pink", main="Histograma de Temperatura", xlab="Temperatura", ylab="Frecuencia")
dev.off()

# 自变量(CH4)直方图
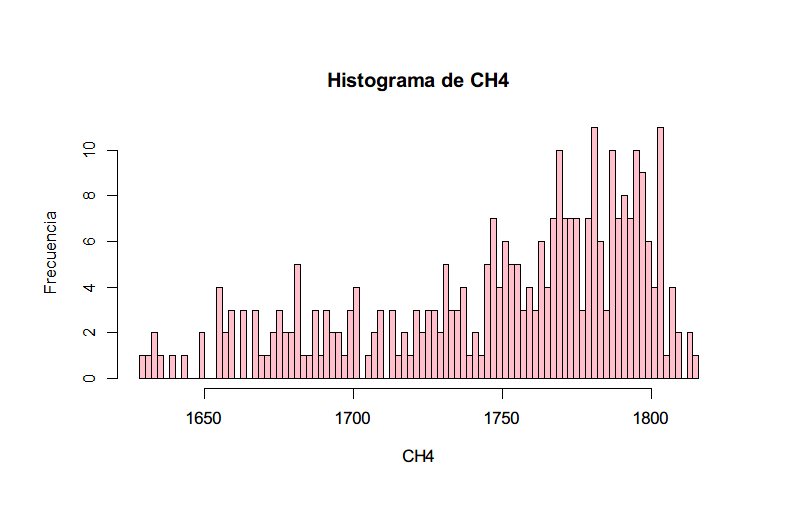
png(file = "./images/hist_CH4.png", width = 800, height = 525, res = 100)
par(oma=c(2,2,2,2))
hist(CH4, breaks=100, col="pink", main="Histograma de CH4", xlab="CH4", ylab="Frecuencia")
dev.off()

# 自变量(CO2)直方图
png(file = "./images/hist_CO2.png", width = 800, height = 525, res = 100)
par(oma=c(2,2,2,2))
hist(CO2, breaks=100, col="pink", main="Histograma de CO2", xlab="CO2", ylab="Frecuencia")
dev.off()

# 自变量(N2O)直方图
png(file = "./images/hist_N2O.png", width = 800, height = 525, res = 100)
par(oma=c(2,2,2,2))
hist(N2O, breaks=100, col="pink", main="Histograma de N2O", xlab="N2O", ylab="Frecuencia")
dev.off()

创建箱线图来检测异常值

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# 检测异常值(Temp)
png(file = "./images/boxplot_Temp.png", width = 800, height = 525, res = 100)
par(oma=c(2,2,2,2))
boxplot(CO2, main="Boxplot de CO2", xlab="CO2", ylab="Frecuencia")
dev.off()

# 检测异常值(CH4)
png(file = "./images/boxplot_CH4.png", width = 800, height = 525, res = 100)
par(oma=c(2,2,2,2))
boxplot(CH4, main="Boxplot de CH4", xlab="CH4", ylab="Frecuencia")
dev.off()

# 检测异常值(CO2)
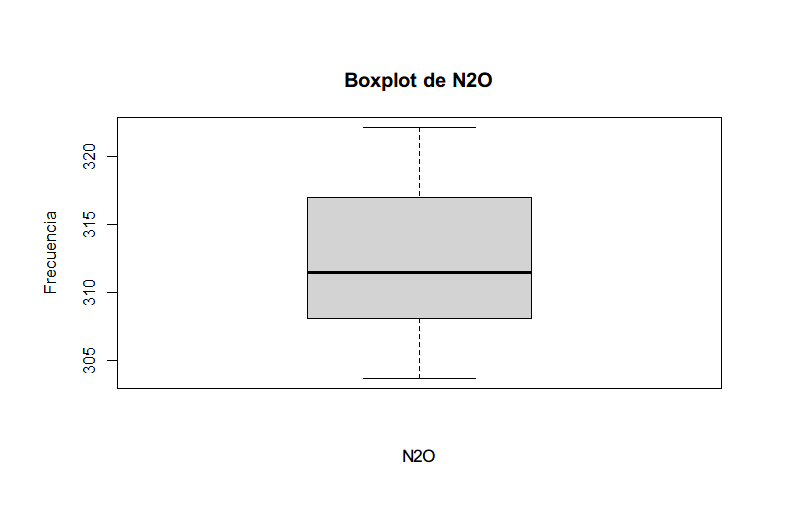
png(file = "./images/boxplot_N2O.png", width = 800, height = 525, res = 100)
par(oma=c(2,2,2,2))
boxplot(N2O, main="Boxplot de N2O", xlab="N2O", ylab="Frecuencia")
dev.off()

# 检测异常值(CO2)
png(file = "./images/boxplot_CO2.png", width = 800, height = 525, res = 100)
par(oma=c(2,2,2,2))
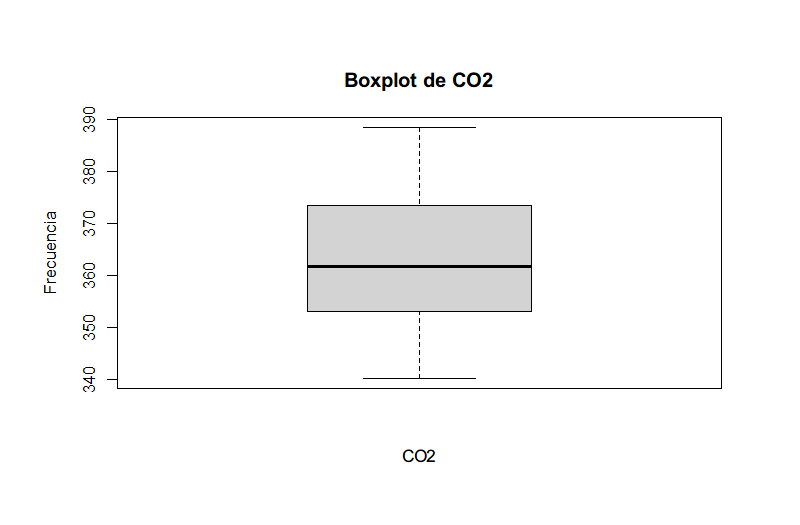
boxplot(Temp, main="Boxplot de Temperatura", xlab="Temperatura", ylab="Frecuencia")
dev.off()

查看相关系数

1
2
# 相关系数
cor(mdata)

1
2
3
4
5
          Temp       CH4       CO2       N2O
Temp 1.0000000 0.6996966 0.7485046 0.7432418
CH4  0.6996966 1.0000000 0.8722531 0.8944092
CO2  0.7485046 0.8722531 1.0000000 0.9811354
N2O  0.7432418 0.8944092 0.9811354 1.0000000

建立线性模型，并打印参数估计的结果，然后进行回归方程的显著性检验

T检验
F检验
调整后的 Adjusted R²

1
2
3
4
# 建立线形模型
modelo <- lm(formula=Temp~CO2+CH4+N2O,data=data)
modelo
summary(modelo)

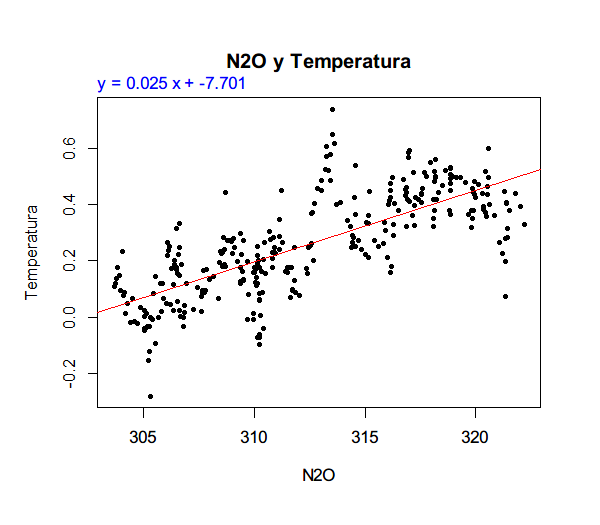
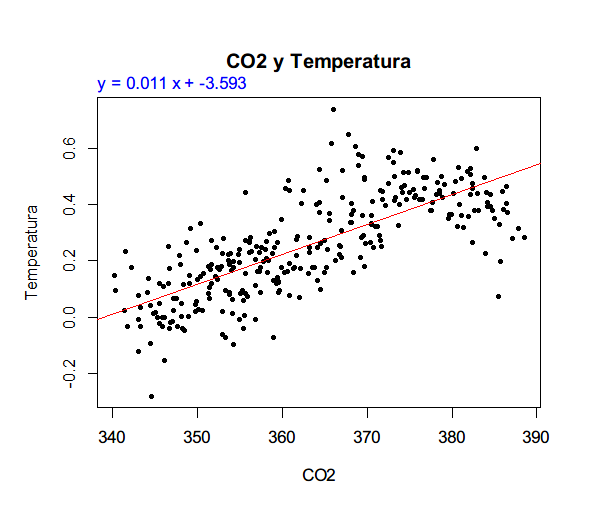
最后，我们通过的回归参数的检验与回归方程的检验，得到最后多元线性回归方程为：

Temp = -4.2676862 + 0.0076848 * CO2 + 0.0007349 * CH4 + 0.0014314 * N2O

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
Call:
lm(formula = Temp ~ CO2 + CH4 + N2O, data = data)

Residuals:
     Min       1Q   Median       3Q      Max
-0.41044 -0.07476  0.00139  0.07208  0.44757

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -4.2676862  1.1577046  -3.686 0.000269 ***
CO2          0.0076848  0.0027617   2.783 0.005729 **
CH4          0.0007349  0.0003278   2.242 0.025699 *
N2O          0.0014314  0.0073093   0.196 0.844868
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1181 on 304 degrees of freedom
Multiple R-squared:  0.5695,    Adjusted R-squared:  0.5652
F-statistic:   134 on 3 and 304 DF,  p-value: < 2.2e-16

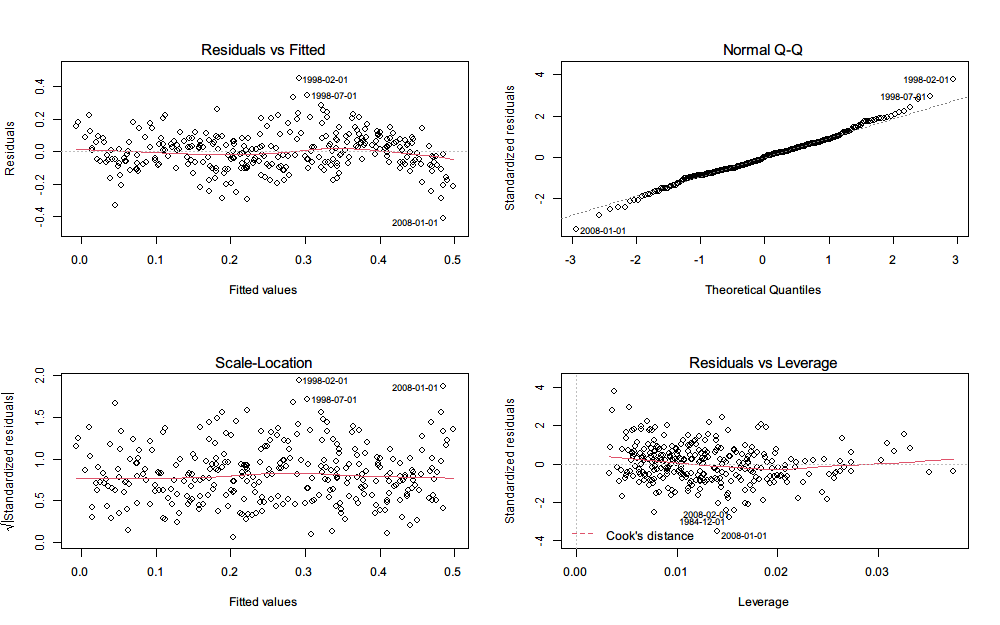
在得到的回归模型进行显著性检验后，还要在做残差分析(预测值和实际值之间的差)，检验模型的正确性，残差必须服从正态分布N(0,σ^2)。直接用plot()函数生成4种用于模型诊断的图形，进行直观地分析。

1
2
3
4
png(file = "./images/residual_analysis.png", width = 1000, height = 625, res = 90)
par(mfrow=c(2,2))
plot(modelo)
dev.off()

逐步回归分析

1
step(modelo)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Start:  AIC=-1312.01
Temp ~ CO2 + CH4 + N2O

       Df Sum of Sq    RSS     AIC
- N2O   1  0.000535 4.2397 -1314.0
<none>              4.2391 -1312.0
- CH4   1  0.070077 4.3092 -1309.0
- CO2   1  0.107975 4.3471 -1306.3

Step:  AIC=-1313.97
Temp ~ CO2 + CH4

       Df Sum of Sq    RSS     AIC
<none>              4.2397 -1314.0
- CH4   1   0.09021 4.3299 -1309.5
- CO2   1   0.78620 5.0259 -1263.6

Call:
lm(formula = Temp ~ CO2 + CH4, data = data)

Coefficients:
(Intercept)          CO2          CH4  
 -4.0469071    0.0081818    0.0007611

计算 R²

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
# 计算去除 CO2 后的R²
modelo_del_CO2 <- lm(formula=Temp~CH4+N2O,data=mdata)
summary(modelo_del_CO2)

# 计算去除 CH4 后的R²
modelo_del_CH4 <- lm(formula=Temp~CO2+N2O,data=mdata)
summary(modelo_del_CH4)

# 计算去除 N2O 后的R²
modelo_del_N2O <- lm(formula=Temp~CO2+CH4,data=mdata)
summary(modelo_del_N2O)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
Call:
lm(formula = Temp ~ CH4 + N2O, data = mdata)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.40339 -0.06894 -0.00508  0.07248  0.44869 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -7.2171582  0.4707278 -15.332   <2e-16 ***
CH4          0.0006792  0.0003308   2.053   0.0409 *  
N2O          0.0201206  0.0029156   6.901    3e-11 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1194 on 305 degrees of freedom
Multiple R-squared:  0.5585,    Adjusted R-squared:  0.5556 
F-statistic: 192.9 on 2 and 305 DF,  p-value: < 2.2e-16



Call:
lm(formula = Temp ~ CO2 + N2O, data = mdata)

Residuals:
     Min       1Q   Median       3Q      Max
-0.41767 -0.07982 -0.00245  0.06403  0.45301

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.934714   1.126173  -4.382 1.62e-05 ***
CO2          0.007307   0.002775   2.633  0.00889 **
N2O          0.008123   0.006716   1.210  0.22740
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1189 on 305 degrees of freedom
Multiple R-squared:  0.5624,    Adjusted R-squared:  0.5595
F-statistic:   196 on 2 and 305 DF,  p-value: < 2.2e-16



Call:
lm(formula = Temp ~ CO2 + CH4, data = mdata)

Residuals:
     Min       1Q   Median       3Q      Max
-0.41026 -0.07505  0.00251  0.07367  0.44738

Coefficients:
              Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.0469071  0.2629079 -15.393  < 2e-16 ***
CO2          0.0081818  0.0010879   7.521 6.14e-13 ***
CH4          0.0007611  0.0002988   2.548   0.0113 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1179 on 305 degrees of freedom
Multiple R-squared:  0.5694,    Adjusted R-squared:  0.5666
F-statistic: 201.7 on 2 and 305 DF,  p-value: < 2.2e-16

进行预测

1
2
3
4
5
nuevos_datos <- data.frame(CH4=1700,CO2=350)
nuevos_datos
pred <- predict(object=modelo_del_N2O, data=nuevos_datos, interval="prediction",level=0.95)
pred
head(pred,10)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
             fit           lwr       upr
1    0.030839372 -2.045871e-01 0.2662658
2    0.023525076 -2.122342e-01 0.2592844
3    0.011943094 -2.236052e-01 0.2474914
4   -0.005025586 -2.404213e-01 0.2303702
5   -0.009066399 -2.432822e-01 0.2251494
6    0.003711027 -2.300327e-01 0.2374547
7    0.009542722 -2.243235e-01 0.2434090
8    0.019159020 -2.149089e-01 0.2532269
9    0.030731635 -2.031753e-01 0.2646386
10   0.034719685 -1.993524e-01 0.2687918

我们得到了多元线性回归方程的公式，就可以对数据进行预测了。我们可以用R语言的predict()函数来计算预测值y0和相应的预测区间，并把实际值和预测值一起可视化化展示。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
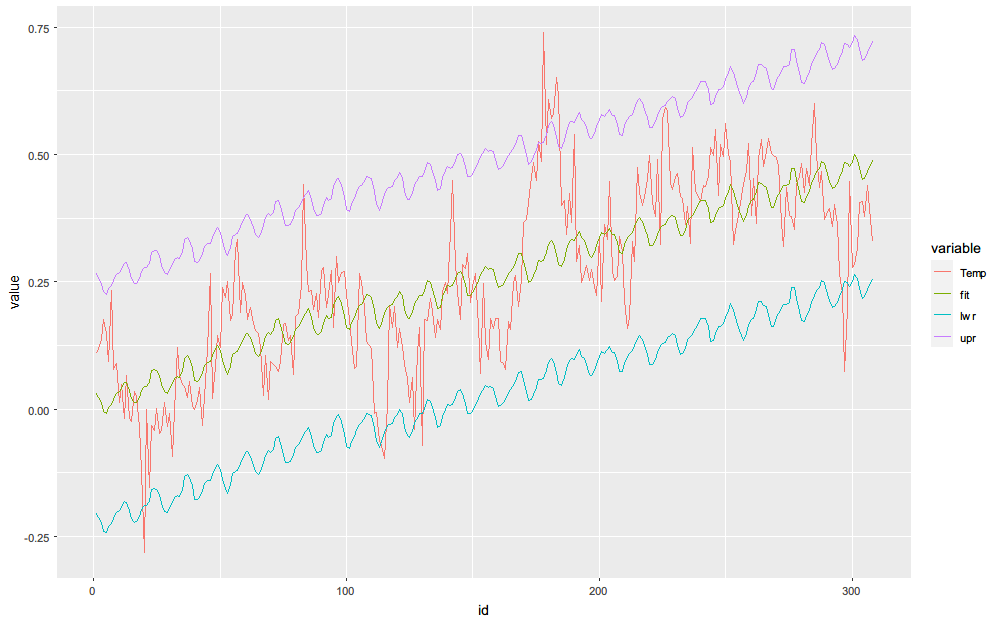
png(file = "./images/prediction.png", width = 1000, height = 625, res = 90)
par(mfrow=c(1,1))
dfp <- data.frame(pred)
head(dfp, 10)
mode(dfp)

mdf<-merge(data$Temp, fit=dfp$fit, lwr=dfp$lwr, upr=dfp$upr)
mdf

# 画图函数
draw <- function(df){
    df2<-data.frame(df)
    df2$id<-index(df2)
    df2$date<-index(df)
    df3<-melt(df2,id=c("id","date"))
    
    g<-ggplot(data=df3,aes_string(x='id',y='value',colour='variable'))
    g<-g+geom_line()
    g
}
draw(mdf)
dev.off()

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
             Temp          fit           lwr       upr
1983-05-01  0.109  0.030839372 -2.045871e-01 0.2662658
1983-06-01  0.118  0.023525076 -2.122342e-01 0.2592844
1983-07-01  0.137  0.011943094 -2.236052e-01 0.2474914
1983-08-01  0.176 -0.005025586 -2.404213e-01 0.2303702
1983-09-01  0.149 -0.009066399 -2.432822e-01 0.2251494
1983-10-01  0.093  0.003711027 -2.300327e-01 0.2374547
1983-11-01  0.232  0.009542722 -2.243235e-01 0.2434090
1983-12-01  0.078  0.019159020 -2.149089e-01 0.2532269
1984-01-01  0.089  0.030731635 -2.031753e-01 0.2646386
1984-02-01  0.013  0.034719685 -1.993524e-01 0.2687918
1984-03-01  0.049  0.039824705 -1.943438e-01 0.2739932
1984-04-01 -0.019  0.051996586 -1.821958e-01 0.2861889
1984-05-01  0.065  0.052022929 -1.828336e-01 0.2868794
1984-06-01 -0.016  0.035790138 -2.002370e-01 0.2718173
1984-07-01 -0.024  0.020863011 -2.152485e-01 0.2569745
1984-08-01  0.034  0.012124223 -2.225349e-01 0.2467834
1984-09-01  0.025  0.012157273 -2.215542e-01 0.2458687
1984-10-01 -0.035  0.023267748 -2.102364e-01 0.2567719
1984-11-01 -0.123  0.036423363 -1.969677e-01 0.2698144
1984-12-01 -0.282  0.044764790 -1.886841e-01 0.2782137
1985-01-01 -0.001  0.043929180 -1.898457e-01 0.2777041
1985-02-01 -0.155  0.052679969 -1.810188e-01 0.2863788
1985-03-01 -0.032  0.075003316 -1.583058e-01 0.3083124

至此，一份简单的多重线性回归就做完了，可以看到我们预测的结果非常的垃圾，模型需要进一步优化，但是我不会，所以就这样凑合交了

至于结果，脚本部分当然是满分啦，其他介绍部分不是我完成的，所以我就不放上来了

El trabajo está bastante bien. Os sugiero para otros trabajos que: numeréis las páginas, pongáis título y número a las tablas y gráficas, mejorar redacción y ser más explícitos en la redacción. (por favor revisad comentarios dentro del texto). Puntuación según apartados:
Introducción (0.25/1)
Especificación (1/1)
Tratamiento, estimación e inter. (2.5/3)
Verificación (2/2.5)
Predicción (1/1)
Script(1.5/1.5)